Utilizing LIGER for the integration of spatial transcriptomic data
Joshua Sodicoff
7/17/2020
Source:vignettes/birs_revised.Rmd
birs_revised.RmdUpdates
This vignette will differ somewhat from my original presentation, namely in that it does not require access to any datasets outside of those provided for the hackathon. Likewise, instead of comparing an analysis across spatial modalities, it will demonstrate the method for generating the results required for that on the conference data. I hope this vignette helps you learn how to use Liger for this task and interpret UMAP plots and clustering metrics to determine the accuracy of your integration
Overview
In this analysis, the additional structure found by combining spatial and single cell transcriptomic datasets with an integrative nonnegative matrix factorization-based method, Liger, is demonstrated. From the separate and integrative analyses, plots of identified and known clusters are generated, metrics of integration performance are compared in context, and it is shown that there is some loss of information as a result of the integration.
#Viewing the data
First, let’s preview the data to ensure that gene features comprise the rows, samples comprise the columns, and known cluster assignments are factor vectors.
tasic[1:10,1:10]
## tasic_1 tasic_2 tasic_3 tasic_4 tasic_5 tasic_6 tasic_7 tasic_8
## abca15 11 42 17 42 35 35 35 42
## abca9 22 46 22 46 39 39 39 46
## acta2 15 47 15 42 34 42 34 47
## adcy4 12 45 12 45 38 38 38 45
## aldh3b2 27 49 27 49 42 42 49 49
## amigo2 23 43 101 43 72 43 43 49
## ankle1 29 46 72 37 61 35 41 24
## ano7 11 42 16 42 34 34 34 42
## anxa9 15 48 15 42 33 42 33 42
## arhgef26 59 43 75 43 36 43 85 49
## tasic_9 tasic_10
## abca15 48 35
## abca9 46 39
## acta2 47 42
## adcy4 45 38
## aldh3b2 49 42
## amigo2 49 43
## ankle1 49 48
## ano7 48 34
## anxa9 48 42
## arhgef26 49 54tasic_clust[1:10]
## tasic_1 tasic_2 tasic_3 tasic_4 tasic_5 tasic_6 tasic_7 tasic_8
## Astrocyte Astrocyte Astrocyte Astrocyte Astrocyte Astrocyte Astrocyte Astrocyte
## tasic_9 tasic_10
## Astrocyte Astrocyte
## 8 Levels: Astrocyte Endothelial Cell ... Oligodendrocyte.3seqfish[1:10,1:10]
## seqfish_1 seqfish_2 seqfish_3 seqfish_4 seqfish_5 seqfish_6 seqfish_7
## abca15 68 49 50 39 31 59 44
## abca9 41 42 38 36 47 18 37
## acta2 25 23 16 21 29 36 21
## adcy4 39 54 37 18 37 26 36
## aldh3b2 101 47 41 52 101 50 101
## amigo2 93 64 93 93 93 93 63
## ankle1 41 42 76 40 46 38 63
## ano7 44 68 50 48 50 46 41
## anxa9 53 40 43 39 31 39 36
## arhgef26 38 40 42 45 46 44 37
## seqfish_8 seqfish_9 seqfish_10
## abca15 66 50 46
## abca9 48 31 41
## acta2 32 25 11
## adcy4 32 33 40
## aldh3b2 56 40 42
## amigo2 56 93 62
## ankle1 27 9 41
## ano7 37 31 46
## anxa9 36 44 82
## arhgef26 45 28 42seq_clust[1:10]
## seqfish_1 seqfish_2 seqfish_3
## Glutamatergic Neuron Glutamatergic Neuron Glutamatergic Neuron
## seqfish_4 seqfish_5 seqfish_6
## Glutamatergic Neuron Glutamatergic Neuron Glutamatergic Neuron
## seqfish_7 seqfish_8 seqfish_9
## Glutamatergic Neuron Glutamatergic Neuron Glutamatergic Neuron
## seqfish_10
## Glutamatergic Neuron
## 8 Levels: Astrocyte Endothelial Cell ... Oligodendrocyte.3Separate integrations
To establish a baseline as the level of structure and clustering accuracy that can be found for each dataset with LIGER, we run individual analyses.
The analysis includes 1. Normalization, to standardize the counts per sample 2. Variable gene selection 3. Scaling, but not centering as not to violate the nonnegativity constraint 4. Integrative non-negative matrix factorization, or essentially just NMF in the case shown here in which one dataset is provided 5. Quantile normalization, primarily used for aligning multiple datasets. 6. Cluster identification with the Louvain algorithm 7. UMAP, for visualization
First, we run the analysis on the scRNA-seq data
tasic_obj = createLiger(list(sc_rnaseq = tasic)) tasic_obj %<>% liger::normalize() %>% liger::selectGenes() %>% liger::scaleNotCenter() %>% liger::optimizeALS(k = 20) %>% liger::quantile_norm() %>% liger::louvainCluster() %>% liger::runUMAP()
Then, we run it on the seqFISH data
seq_obj = createLiger(list(spatial = seqfish)) seq_obj %<>% liger::normalize() %>% liger::selectGenes() %>% liger::scaleNotCenter() %>% liger::optimizeALS(k = 20) %>% liger::quantile_norm() %>% liger::louvainCluster() %>% liger::runUMAP()
We then plot the evaluated data by generated and known cluster for the scRNA-seq
names(tasic_obj@clusters) = colnames(tasic) tasic_plots = plotByDatasetAndCluster(tasic_obj, return.plots = T) tasic_plot_known_clust = plotByDatasetAndCluster(tasic_obj, clusters = tasic_clust, return.plots = T) tasic_plots[[2]]
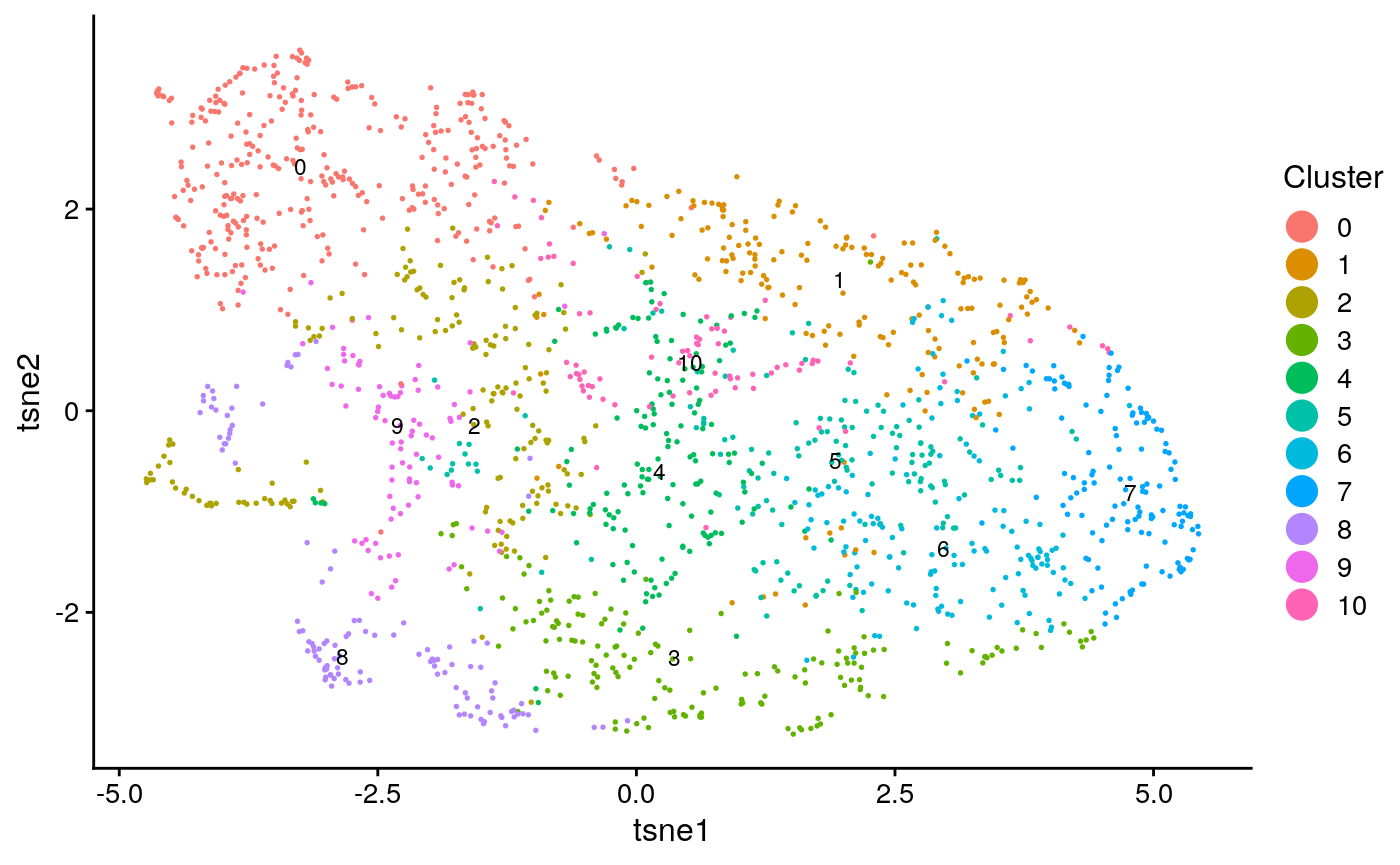
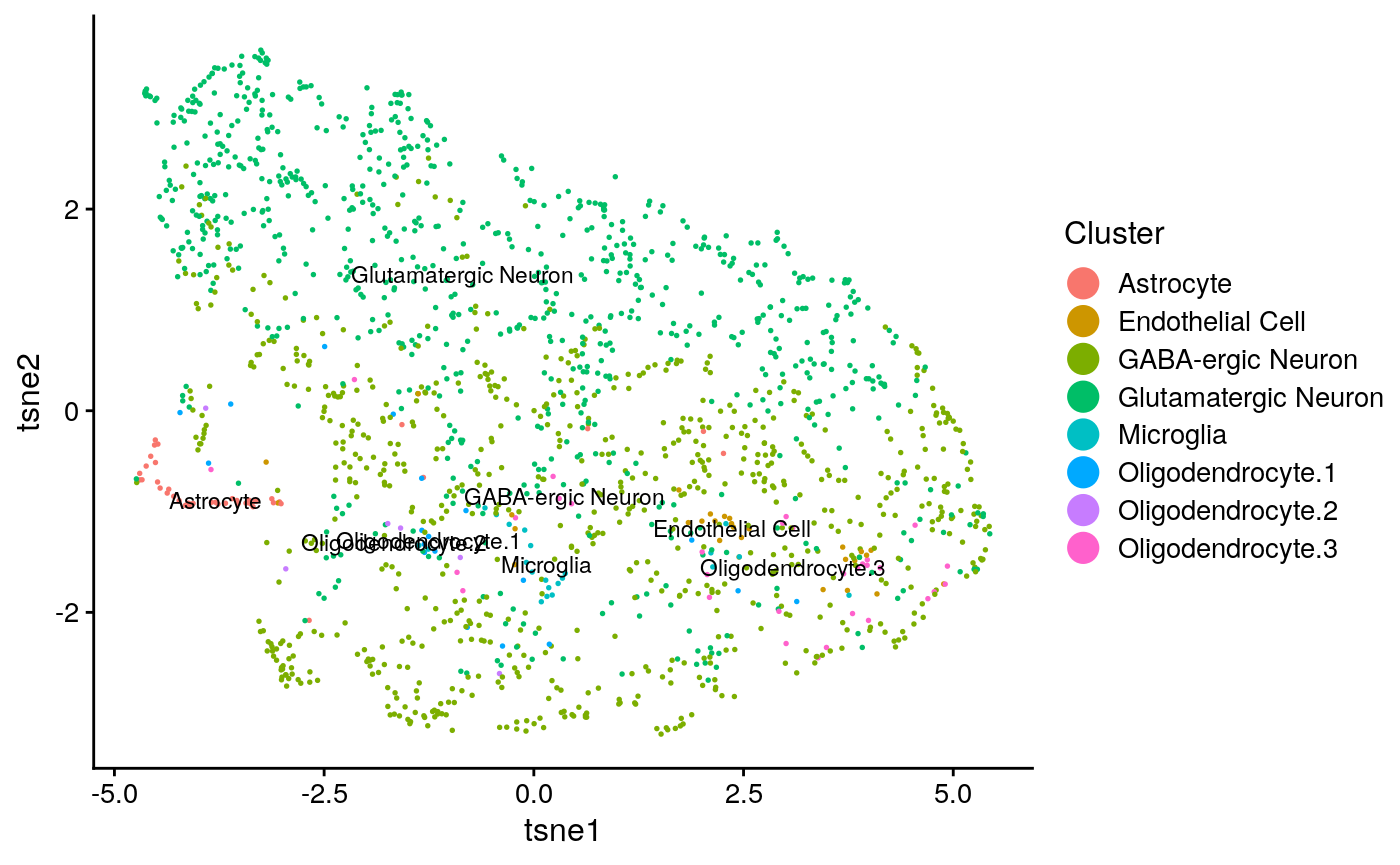
tasic_plot_known_clust[[2]]
and then the spatial data
names(seq_obj@clusters) = colnames(seqfish) seq_plots = plotByDatasetAndCluster(seq_obj, return.plots = T) seq_plot_known_clust = plotByDatasetAndCluster(seq_obj, clusters = seq_clust, return.plots = T) seq_plots[[2]]
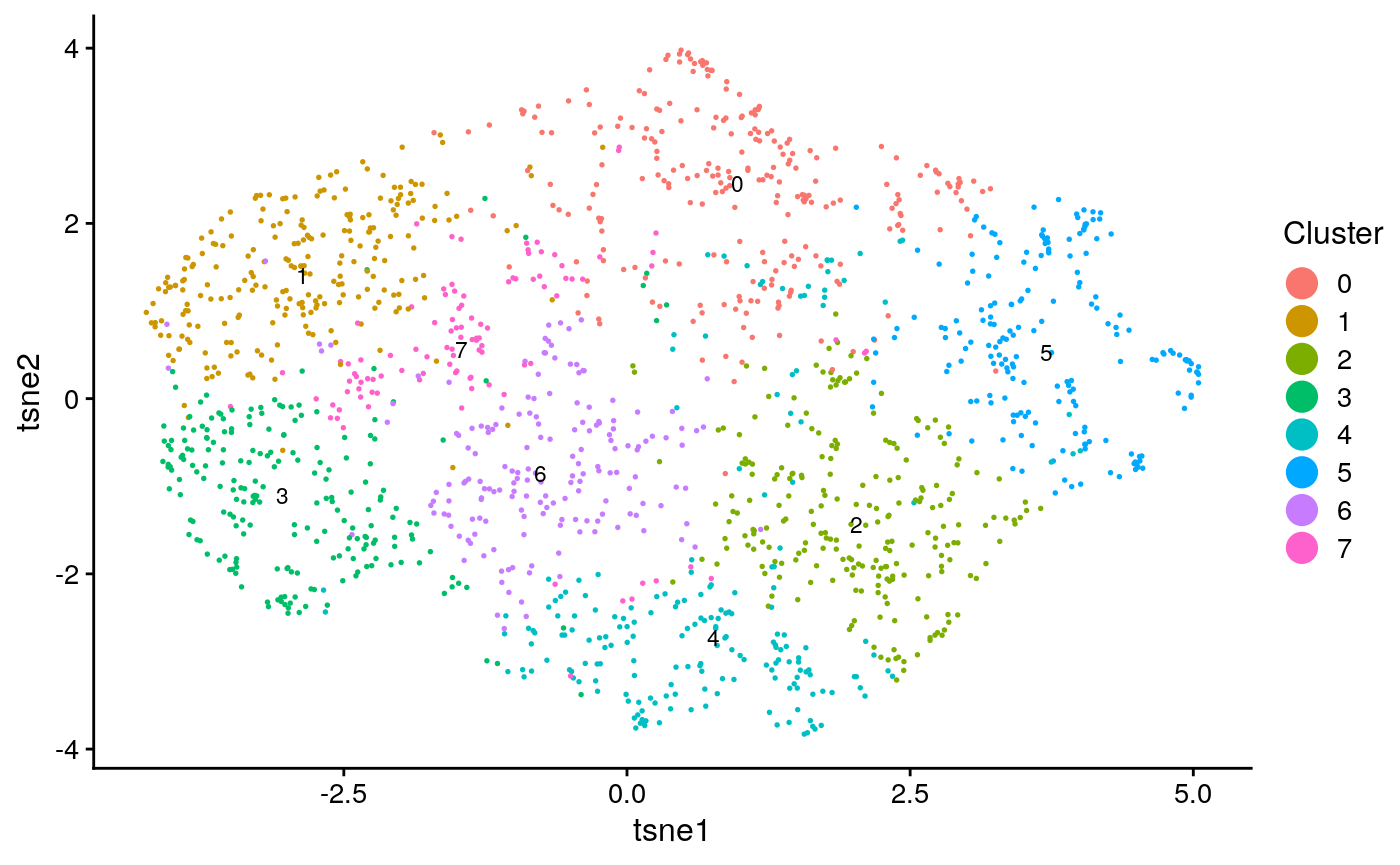
seq_plot_known_clust[[2]]
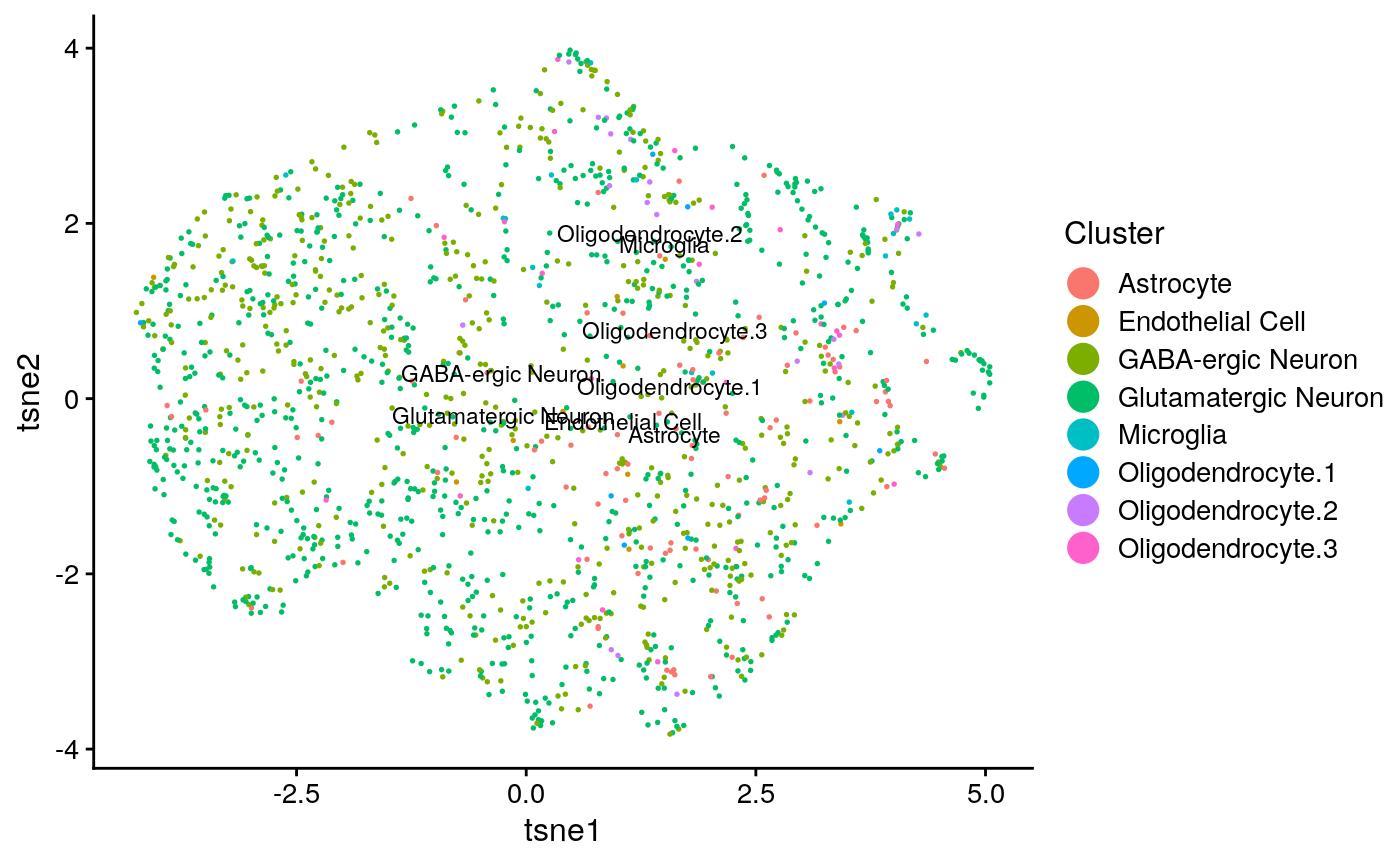We can make a few qualitative obeservations: * Neither analysis seems to have a lot of structure, resulting in the UMAP plots coming out rather “blobby”. * The known clusters in the scRNA-seq seem to map slightly better to the generated clusters than the spatial data.
We calculate metrics of clustering accuracy to compare. ARI is the adjusted Rand index, a metric based on the number of cell-cell pairs known to reside in the same and different clusters and adjusted to account for random chance. Purity is found by dividing the total number of correctly identified cells in a cluster over the total number of cells in that cluster.
## [1] "tasic ARI: 0.124928479183329"## [1] "tasic purity: 0.737086477074869"## [1] "seqfish ARI: 0.00922479431962868"## [1] "seqfish purity: 0.546023794614903"This confirms that the single cell data had somewhat better clustering accuracy.
Now, let’s try to integrate the datasets, using almost the same workflow as before but with both datasets provided for object creation.
int_obj = createLiger(list(sc_rnaseq = tasic, spatial = seqfish)) int_obj %<>% liger::normalize() %>% liger::selectGenes() %>% liger::scaleNotCenter() %>% liger::optimizeALS(k = 20) %>% liger::quantile_norm() %>% liger::louvainCluster() %>% liger::runUMAP()
Again, we plot the output, including one showing dataset of origin
names(int_obj@clusters) = c(colnames(tasic), colnames(seqfish)) int_clust = as.factor(c(as.character(tasic_clust), as.character(seq_clust))); names(int_clust) = c(names(tasic_clust), names(seq_clust)) int_plots = plotByDatasetAndCluster(int_obj, return.plots = T) int_plot_known_clust = plotByDatasetAndCluster(int_obj, clusters = int_clust, return.plots = T) int_plots[[1]]
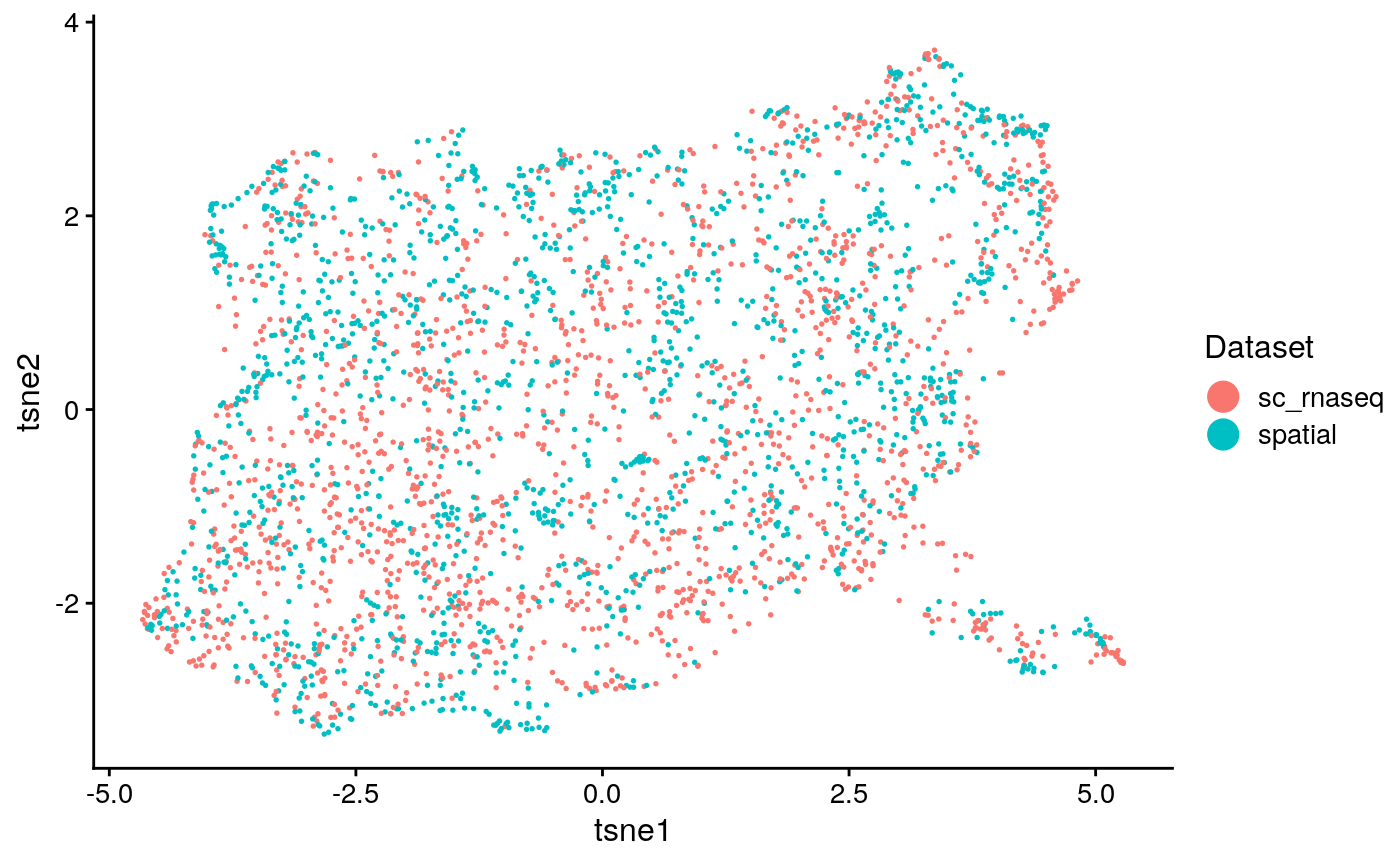
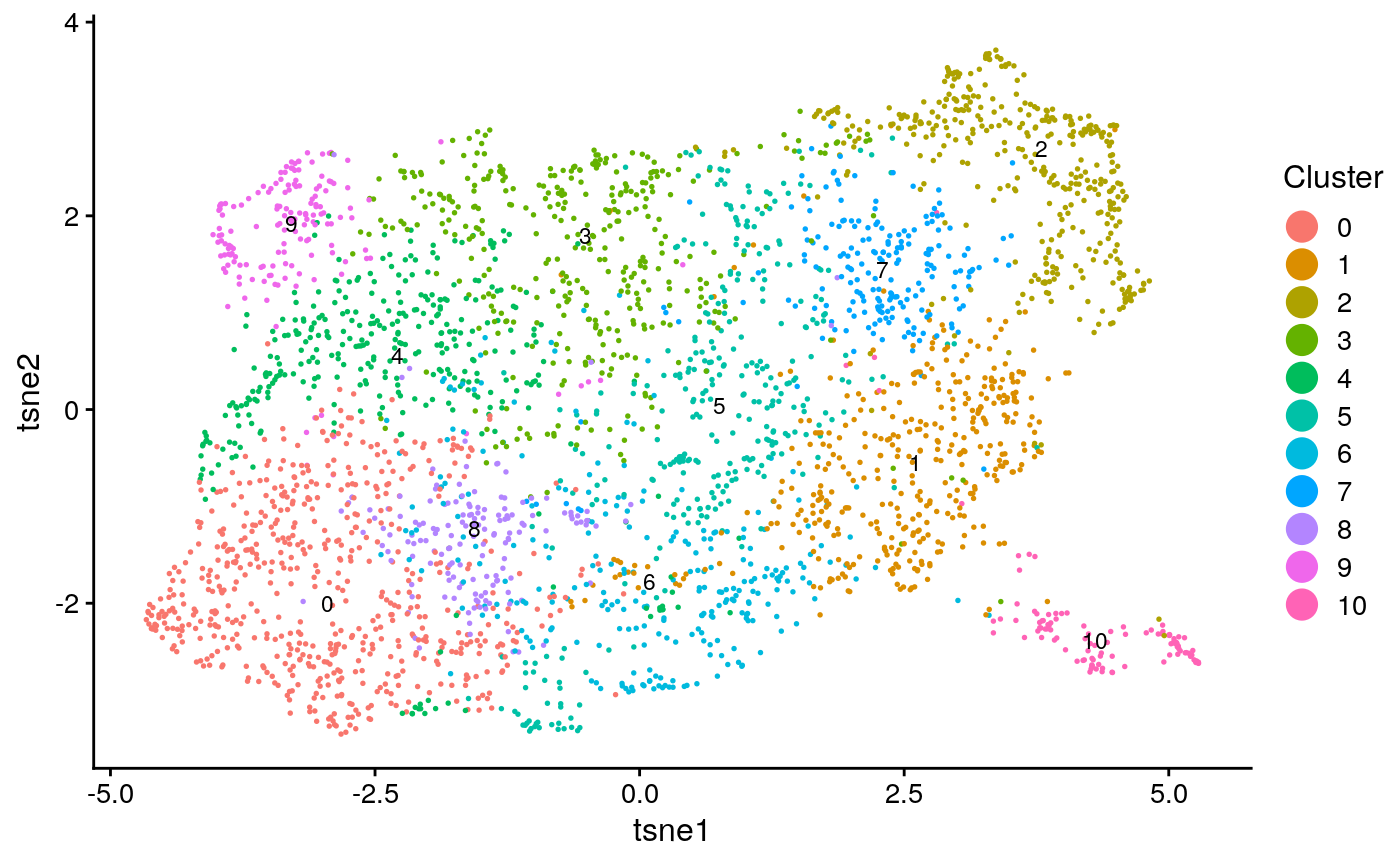
int_plots[[2]]
int_plot_known_clust[[2]]
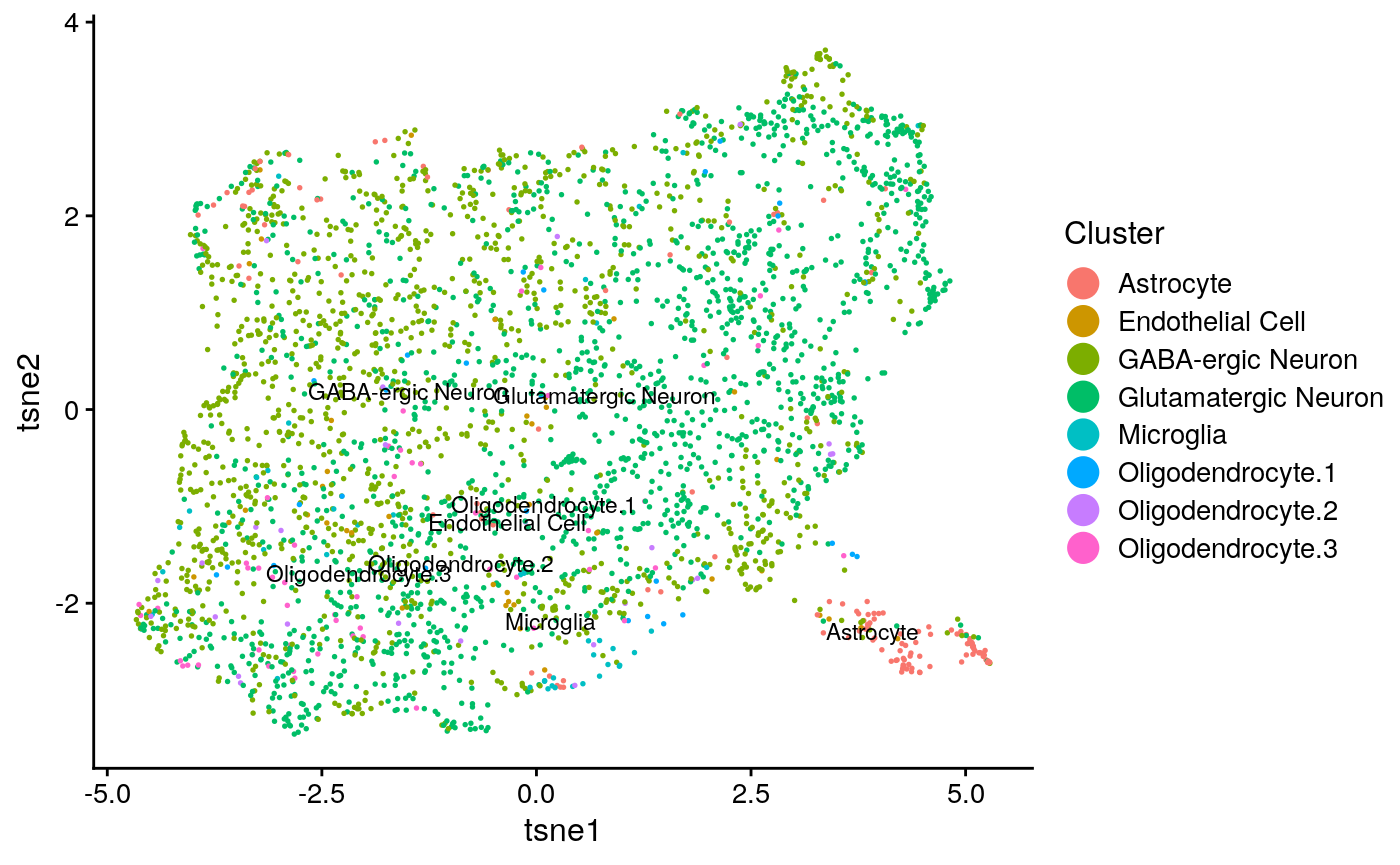
We calculate clustering accuracy, as well as agreement and alignment
## [1] "overall ARI: 0.03990832682262"## [1] "overall purity: 0.621084337349398"## [1] "Reducing dimensionality using NMF"
##
## Converged in 0.01860118 seconds, 167 iterations. Objective: 5408.016
##
## Converged in 0.01765323 seconds, 188 iterations. Objective: 8577.805
## [1] "agreement: 0.089592886480605"## [1] "alignment: 0.804064439004953"This seems to demonstrate that the clustering accuracy of the integration (a surrogate for how well the method divided the cell types) falls somehwere between solely using the spatial data and scRNA-seq. Additionally, the agreement metric is relatively low (on its scale of 0 to 1). This implies that the integration was not very informative and relied heavily on distortion of the data for alignment.